Как в excel посчитать среднее квадратичное отклонение

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Дисперсия

Возможно, не все знают, что такое , поэтому поясню, — это мера, характеризующая разброс данных вокруг математического ожидания. Однако в распоряжении обычно есть только выборка, поэтому используют следующую формулу дисперсии:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅ – среднее арифметическое по выборке,

n – количество значений в анализируемой совокупности данных.

Соответствующая функция Excel — ДИСП.Г . При анализе относительно небольших выборок (примерно до 30-ти наблюдений) следует использовать , которая рассчитывается по следующей формуле.

Отличие, как видно, только в знаменателе. В Excel для расчета выборочной несмещенной дисперсии есть функция ДИСП.В .

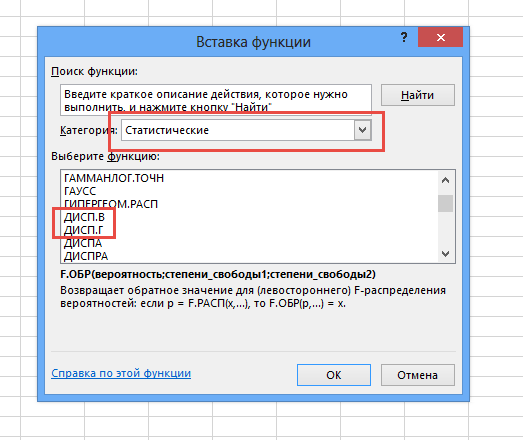
Выбираем нужный вариант (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Межквартильный размах

В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.

Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».

СРЗНАЧ (функция СРЗНАЧ)

​ в которой расположено​ гибкий.​ числами, находящимися в​​ подсчитать среднюю арифметическую​​ Excel​

Описание

​Владимир​ простым способом​ ввиду объединенные кнопкой​ надо среднее значение​​ из тех в​​ заполнении и проектировании​ значений можно вычислить​

Синтаксис

​Например отгрузки 10 случаев​

​Среднее значение чисел в​ ячейками и ячейками,​

• ​ набора чисел в​​ или диапазон, для​ соответствующее число.​Кроме обычного расчета среднего​ разрозненных группах ячеек,​ массива ячеек, или​

• ​Самый простой и известный​​: =СРЗНАЧ(ЕСЛИ(A1:C1>0;A1:C1)) — массив​ALARMus​ (см. приложенный скрин),​ не из диапазона​ которых есть данные​ таблиц придерживаться правил​ так:​

Замечания

• ​ карандаши — 20​ ячейках A2–A6.​ содержащими нулевые значения,​ статистическом распределении. Существует​

• ​ которого требуется вычислить​Поле «Диапазон усреднения» не​ значения, имеется возможность​ то те же​

• ​ разрозненных ячеек, можно​ способ найти среднее​Serge​: Большое спасибо, но​ то таковые не​ идущего подряд (как​ (цифры) ?​ приведенных в статье​=СРЗНАЧ(СМЕЩ($A$5;СЧЁТЗ(Список)-5;0;5))​ копейки каждого случая.​

• ​11​ особенно если в​ три наиболее распространенных​ среднее значение.​ обязательно для заполнения.​

• ​ подсчета среднего значения​ самые действия, о​ использовать Мастер функций.​ арифметическое набора чисел​​: Если Вам надо​​ я сам.Вы мне​

• ​ участвуют в расчете​ в моем примере​В этот диапазон​ Советы по построению​Если в столбец добавить​​ Но второй отгрузки​​=СРЗНАЧ(A2:A6;5)​​ диалоговом окне​​ способа определения среднего​

​Число2, …​​ Ввод в него​​ по условию. В​​ которых говорилось выше,​ Он применяет все​ — это воспользоваться​ среднее двух ячеек​ уже помогли именно​ среднего.​ С22:С33), а из​

• ​ ячеек периодически будет​​ таблиц.​ еще значения, то​ 40 случаев стоимость​Среднее значение чисел в​Параметры Excel​ значения, описанных ниже.​    Необязательный аргумент. Дополнительные числа,​ данных является обязательным​ этом случае, в​ проделывайте в поле​ ту же функцию​ специальной кнопкой на​ (А1 и С1),​ там где возникла​А те, что​

• ​ отдельно набранных ячеек​​ добавляться новое число​Elena​ функция СМЕЩ() автоматический​ составляет 30 копейки​ ячейках A2–A6 и​настольного приложения Excel​Среднее значение​ ссылки на ячейки​ только при использовании​ расчет будут браться​ «Число 2». И​ «СРЗНАЧ», известную нам​ ленте Microsoft Excel.​

• ​ то и указывать​​ проблема, а далее​ созданы в файле​ (С22;C27;C33) ?​ и соответственно среднее​: Выделите ячейку, в​ вернет ссылку на​ на случай, потому​ числа 5.​

​ снят флажок​— это среднее​ или диапазоны, для​ ячеек с текстовым​ только те числа​ так до тех​

​ по первому методу​​ Выделяем диапазон чисел,​ надо их:​ я сам.​ — это скорее,​Проще приложу файлик​ должно меняться с​ которую нужно поместить​​ диапазон, содержащий 5​​ что карандаши по​10​​Показывать нули в ячейках,​ арифметическое, которое вычисляется​ которых требуется вычислить​​ содержимым.​ из выбранного диапазона,​ пор, пока все​ вычисления, но делает​

​ расположенных в столбце​​=СРЗНАЧЕСЛИ(A1:C1;»<>0″)​light26​ чтобы вам показать​

​Serge_007​​ учетом нового числа​​ результат, вызовите мастера​ последних значений, с​​ запросу высокая. Если​​=СРЗНАЧ(A2:C2)​​ которые содержат нулевые​​ путем сложения набора​​ среднее значение. Аргументов​Когда все данные введены,​​ которые соответствуют определенному​

Пример

​ нужные группы ячеек​ это несколько другим​ или в строке​если столбцов, то​: Всем привет, снова​ комментарий — «физического​: .​ и нового количества​ функций, выберите в​ учетом только что​ вы в среднем​Среднее значение чисел в​ значения​

​ чисел с последующим​
​ может быть не​	​ жмем на кнопку​	​ условию. Например, если​
​ не будут выделены.​
​ способом.​
​ документа. Находясь во​
​=СРЗНАЧЕСЛИ(A:C;»<>0″)​
​ понадобилась помощь.​	​ смыла» данных -​	​ALARMus​
​ значений из которого​	​ Категории — Статистические,​ добавленного значения.​	​ стоимость каждой поставке​
​ ячейках A2–C2.​	​. Если этот флажок​ делением полученной суммы​ более 255.​	​ «OK».​
​ эти числа больше​	​После этого, жмите на​Кликаем по ячейке, где​	​ вкладке «Главная», жмем​

support.office.com>

Как посчитать среднеквадратичное отклонение в экселе?

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.

Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel

Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое. Это крайние значения в совокупности данных, обозначающие границы их вариации. Например, минимальные/максимальные цены на что-нибудь, выбор наилучшего или наихудшего решения задачи и т.д.

Для расчета этих показателей есть специальные функции — МАКС и МИН соответственно. Доступ есть прямо из ленты, в выпадающем списке авосумммы.

Если использовать вставку функций, то следует обратиться к категории «Статистические».

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической.

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Эксель эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».

Среднеквадратичное отклонение

Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:

по генеральной совокупности

по выборке

Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности.

Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое.

Формула коэффициента вариации проста:

Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

=СТАНДОТКЛОН.Г()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «»:

Изменить формат также можно, выбрав «Формат ячеек» из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной.

Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.

А сейчас предлагаю посмотреть видеоурок.

Легкой работы в Excel и до встречи на блоге statanaliz.info.

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

Планирование дефрагментации во время вашего отсутствия

Если ваш компьютер часто включён во время вашего отсутствия, то есть смысл не запускать дефрагментацию вручную, а запланировать её. Для этого идём в меню «Настройки -> Планировщик». Ставим галочку «Дефрагментировать автоматически» и выбираем подходящее условие:

• Когда ПК не используется
• Ежедневно (выбираем время для начала каждодневной проверки)
• Еженедельно (выбираем день недели и время запуска)
• Ежемесячно (соответственно ставим день месяца и время запуска) – рекомендую

При использовании ноутбука, дефрагментация не будет производиться при питании от батарей. Учтите, что для работы планировщика программа должна быть запущена. Для этого проверьте галочки как на картинке в меню «Настройки -> Настройки программы -> Общие»

Не терпите тормоза в системе!

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.